Včera som hľadala akési papiere. Ako to tak býva, nenašla som to, čo som hľadala, ale niečo iné. Našla som jeden šanón, ktorý som si odložila z čias, keď som chodila na vysokú. Boli v ňom okopírované časopisy DM (didaktika matematiky), ktoré vytváral a sám aj tlačil náš nezabudnuteľný učiteľ Dušan Jedinák. V jednom z nich je úloha, ktorá ma inšpirovala k napísaniu tohto príspevku – Buffonova úloha o ihle.
Buffonovu úlohu o ihle vytvoril Georges Louis Leclerc de Buffon v roku 1777. Bol to francúzsky matematik, prírodovedec a spisovateľ (výborná kombinácia 😉). V úlohe ide o to, vypočítať, aká je pravdepodobnosť, že keď hodím ihlu na zem, na ktorej sú vyznačené rovnobežné priamky všetky rovnako od seba vzdialené, že táto ihla pretne niektorú z tých priamok.
Skôr než sa pustím do riešenia, neodpustím si zamyslenie nad tým, ako táto úloha asi vznikla. Predstavujem si pána Buffona, ako si zašíva ponožky v miestnosti s podlahou z drevených dosák. Všetky dosky sú rovnako široké a dosť dlhé na to, aby vystačili na celú šírku miestnosti. Nitka sa minula, treba navliecť novú a šup. Ihla spadla na zem tak, že práve v jej strede pretla škáru medzi doskami. To ho zaujalo. Aká je pravdepodobnosť, že sa toto stane? Skúsi hodiť ihlu ešte pár krát. Ihla niekedy padne na škáru, niekedy nie. A tak vymyslí úlohu, ktorá ponesie jeho meno.

Možno to tak bolo, možno nie. Keďže som si to práve teraz vymyslela, tak skôr nie. 😁 Newtonovi tiež jablko na hlavu pravdepodobne nepadlo.
Ja by som ale zadanie rozšírila o ďalšiu otázku. Spravila by som z toho súťaž. Dvaja hádžu na zem ihlu (nazývam ju ihla, ale z bezpečnostných dôvodov by som pri praktickej realizácii použila nejakú neostrú paličku). Na zemi sú rovnobežné čiary vždy 10 cm od seba. Keď hráč trafí čiaru, má bod. Je to férová súťaž – obaja majú rovnaké šance. V tom ale jeden z hráčov navrhne, že si to sťaží. Bude hádzať polovičnou ihlou, ale za každé trafenie dostane dva body. Je jeho návrh férový?
Riešenie
Teraz môžeme prejsť k samotnému výpočtu. Máme tu niekoľko premenných. Nevieme, kam ihla dopadne – budeme uvažovať o vzdialenosti stredu ihly od najbližšej čiary. Túto premennú nazveme d a je jasné, že môže mať hodnoty od nuly do 5 cm, keďže čiary sú od seba vzdialené 10 cm. Druhou premennou bude uhol, ktorý bude ihla zvierať s čiarami. Tento môže byť medzi nulou a pravým uhlom, čiže π/2. Pri hádzaní sú tieto dve premenné nezávislé – neovplyvňujú sa. To, kam padne ihla nemá vplyv na uhol, ani naopak. V prípade, že ihla pretne čiaru, platí vzťah medzi týmito dvoma premennými. Ten je odvodený na obrázku. Aha, ešte je tu h – dĺžka ihly. Tú si predstavíme ako nejaké konkrétne číslo, zatiaľ nevieme, aké.
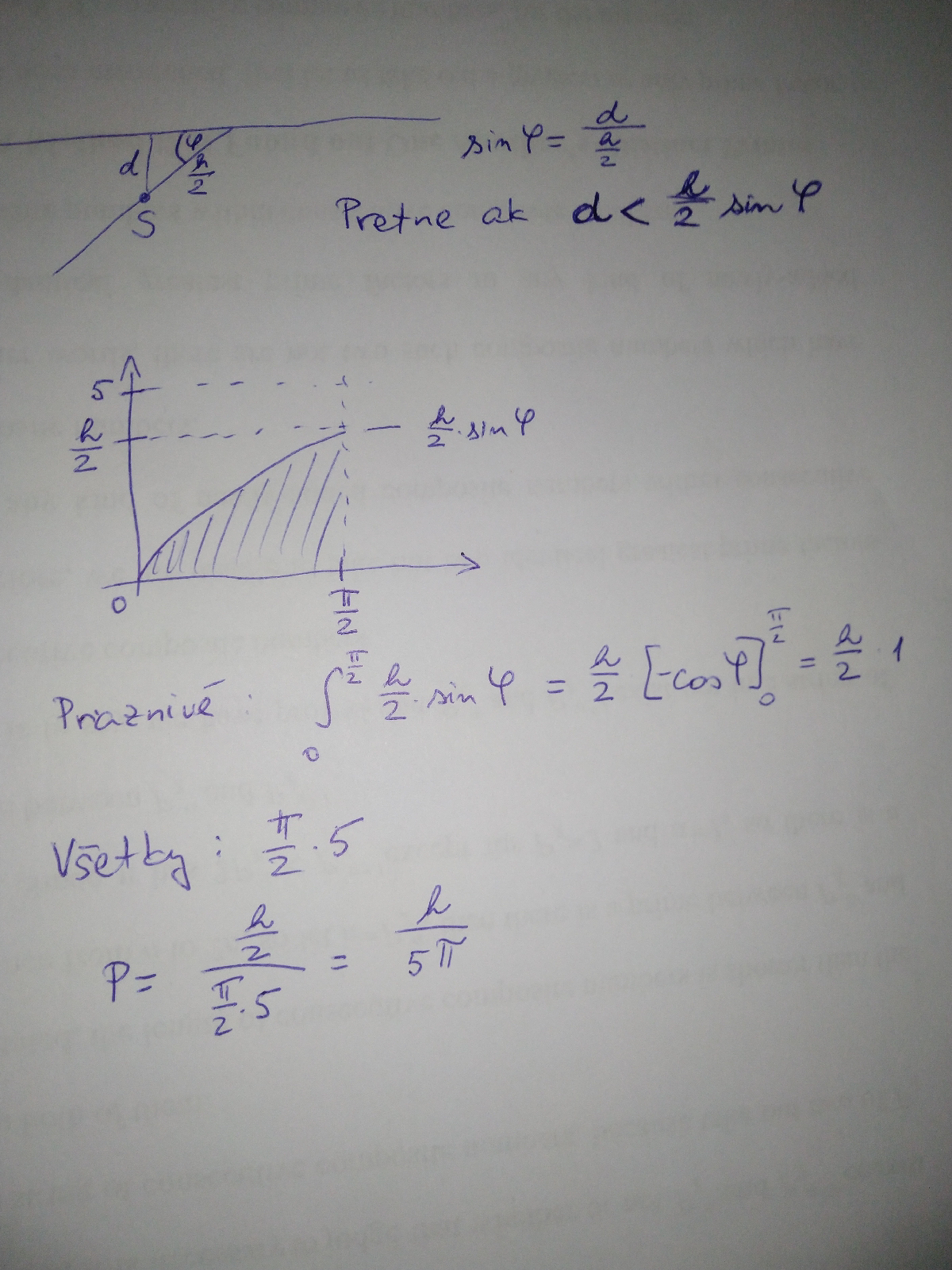
No a keď chceme vypočítať pravdepodobnosť, musíme určiť počet priaznivých prípadov a počet všetkých možných prípadov. V tejto úlohe sú oba nekonečné – ihla môže dopadnúť kamkoľvek a aj pretnúť čiaru kdekoľvek.
V takýchto prípadoch nám skvele pomôže geometrická pravdepodobnosť. Premenné zmeníme na geometrické objekty, a tak určíme veľkosť množiny priaznivých udalostí aj množiny všetkých možných udalostí. Keďže máme dve premenné, pôjde o plochy. Veľkosť množiny všetkých možných udalostí je obsahom obdĺžnika so stranami 5 cm za premennú d a π/2 za uhol. Množinu priaznivých udalostí určíme ako veľkosť plochy pod čiarou, ktorá určuje vypočítaný vzťah medzi týmito dvoma premennými. Spomenieme si, ako sa počíta určitý integrál a výsledok je za chvíľu na svete.
Pravdepodobnosť je teda h/5π. Rastie priamoúmerne s dĺžkou ihly, až kým ihla nebude dlhšia, než je vzdialenosť čiar. (Tam by sa musel upraviť výpočet geometrickej pravdepodobnosti.) S polovičnou ihlou bude teda naozaj polovičná pravdepodobnosť a teda návrh je férový. Zaujímavé je, že ak by sme zvolili ihlu dĺžky 5 cm – polovica vzdialenosti rovnobežiek, tak pravdepodobnosť je 1/π. Tým dostávame pekný spôsob, ako približne určiť hodnotu čísla π. Stačí veľmi veľmi veľa krát hádzať ihlu na zem s rovnobežkami a zapisovať, koľkokrát ihla pretla nejakú čiaru. 😉
